A Compositional Framework for Scientific Model Augmentation¶

- Teaching computers to do science
- Model Augmentation and Synthesis
- Arbitrary models are complex, but transformations are simpler
- Project Repo github.com/jpfairbanks/SemanticModels.jl
Machine Augmentation of Scientists¶
- Scientists are busy writting papers
- Papers are a low bandwidth medium, because of imprecision
- We want to build AI scientists
Science as nested optimization¶
Fitting the data is a regression problem:
$$\ell^* = \min_{h\in {H}} \ell(h(x), y)$$
Institutional process of discovery is
$$\max_{{H}\in \mathcal{M}} expl(h^*)$$ where expl is the explanatory power of a class of models $H$.
- The explanatory power is some combination of
- generalization,
- parsimony,
- and consistency with the fundamental principles of the field.
Modeling Frameworks¶
Most frameworks are designed before the models are written
| Domain | ||
|---|---|---|
| Algebra |  |
 |
| Learning |  |
 |
| Optimization |  |
|
| Modeling |  |
 |
SemanticModels is a post hoc modeling framework
Statistical / ML models are accurate¶
Fitting curves to data is good, but doesn't explain the data.
Scientific Models are Mechanistic¶
Mechanistic models are more explainable than black box or statistical models. They posit driving forces and natural laws that drive the evolution of systems over time.
We call these simulations when necessary to distinguish from model
- Benefits: more explainable, more generalizable
- Cons: lower Accuracy, less flexible
SIR model of disease¶
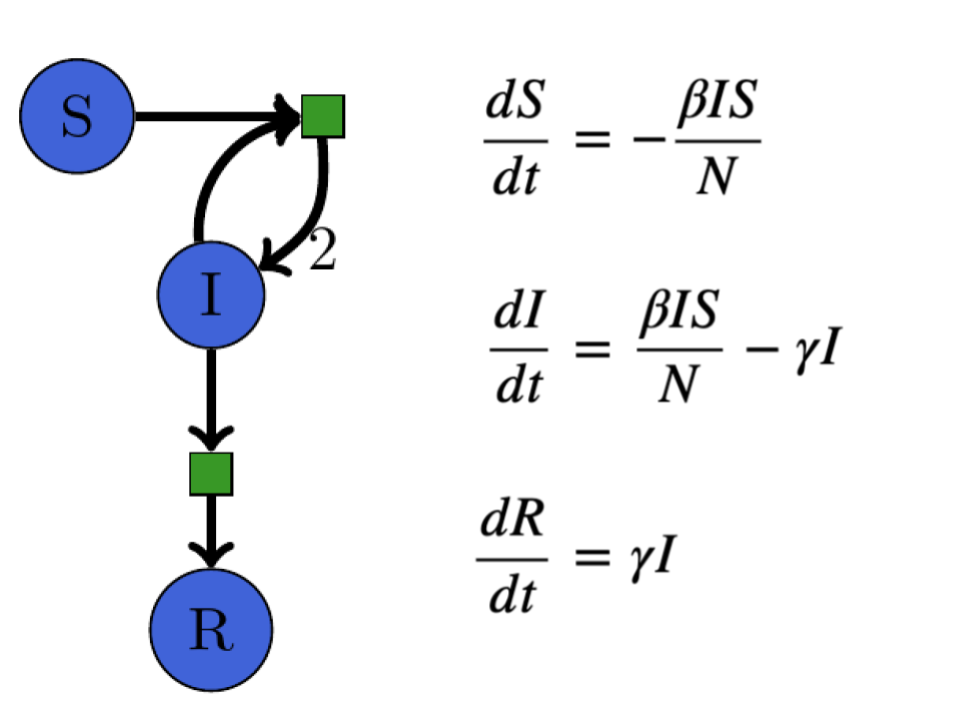 A Petri net -> ODE equivalence
A Petri net -> ODE equivalence
Predictions¶
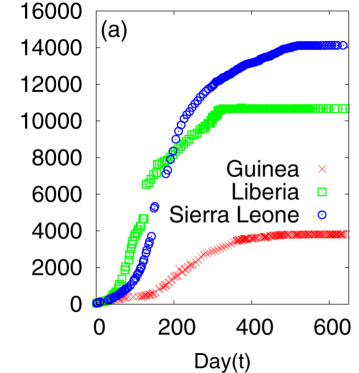 Ebola Outbreak Data
Ebola Outbreak Data
(a) Cumulative number of infected individuals as a function of time (day) for the three countries Guinea, Liberia and Sierra Leone.
A Khalequea, and P Senb, "An empirical analysis of the Ebola outbreak in West Africa" 2017
ODE Based Implementation¶
This is a "real world" implementation of SIR modeling in Julia taken from Epirecipes Cookbook (Simon Frost)
module SIRModel
using DifferentialEquations
function sir_ode(du, u, p, t)
#Infected per-Capita Rate
β = p[1]
#Recover per-capita rate
γ = p[2]
#Susceptible Individuals
S = u[1]
#Infected Individuals
I = u[2]
du[1] = -β * S * I
du[2] = β * S * I - γ * I
du[3] = γ * I
end
#Param = (Infected Per Capita Rate, Recover Per Capita Rate)
param = [0.1,0.05]
#Initial Params = (Susceptible Individuals, Infected by Infected Individuals)
init = [0.99,0.01,0.0]
tspan = (0.0,200.0)
sir_prob = ODEProblem(sir_ode, init, tspan, param)
sir_sol = solve(sir_prob, saveat = 0.1);
Agent based simulation¶
""" Agent Models is a hypothetical ABM framework"""
module AgentModels
abstract type AgentModel end
mutable struct StateModel <: AgentModel
states
agents
transitions
end
solve(m::StateModel) = return thesolution(m)
end
using AgentModels #<- hypothetical ABM framework
numinfected() = sum(a.==:I)
infection(x) = rand(Float64) < numinfected() ? :I : :S
recovery(x) = rand(Float64) < ρ ? :I : :R
function main(nsteps)
n = 20
a = fill(:S, n)
ρ = 0.5 + randn(Float64)/4 # chance of recovery
μ = 0.5 # chance of immunity
T = Dict(S=>infection, I=>recovery)
sam = StateModel([:S, :I, :R], a, T, zeros(Float64,3))
distribution = solve!(sam, nsteps)
return distribution
end
main(150)
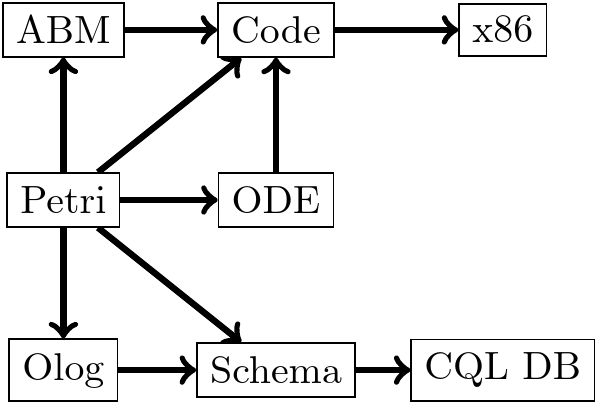
Model Augmentation as a Lens¶
We want scientists to program using lenses
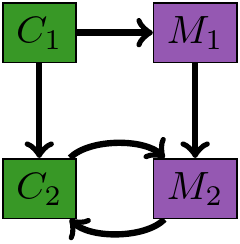 Module Augmentation as a Lens
Module Augmentation as a Lens
What should the $M_1, M_2$ be?
Objects from a Category!¶
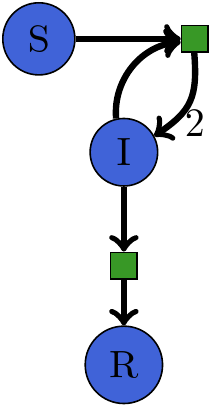 Petri Net for SIR
Petri Net for SIR
Petrinet SIR Model¶
using Petri
function main()
@variables S, I, R
N = +(S,I,R)
Δ = [(S+I, 2I),
(I, R)]
m = Petri.Model(Δ)
p = Petri.Problem(m, SIRState(100, 1, 0), 50)
soln = Petri.solve(p)
(p, soln)
end
p, soln = main()
Semantic Models Applies Category Theory¶
A novel modeling environment that builds and manipulates models in this category theory approach.
Contributions:
- We take general code as input
- Highly general and extensible framework
- Goal: Transformations are compositional
Converting Models between Categories¶
Models can be represented in different categories, for example, SIR as an OLOG.
Type Graphs¶
- The TypeGraph of a Julia Program looks a lot like the OLOG of the program it runs
- Computers are good at type checking
- Can we embed our semantics into the type system?
Functorial Semantics?¶
Can we make this rigorous?
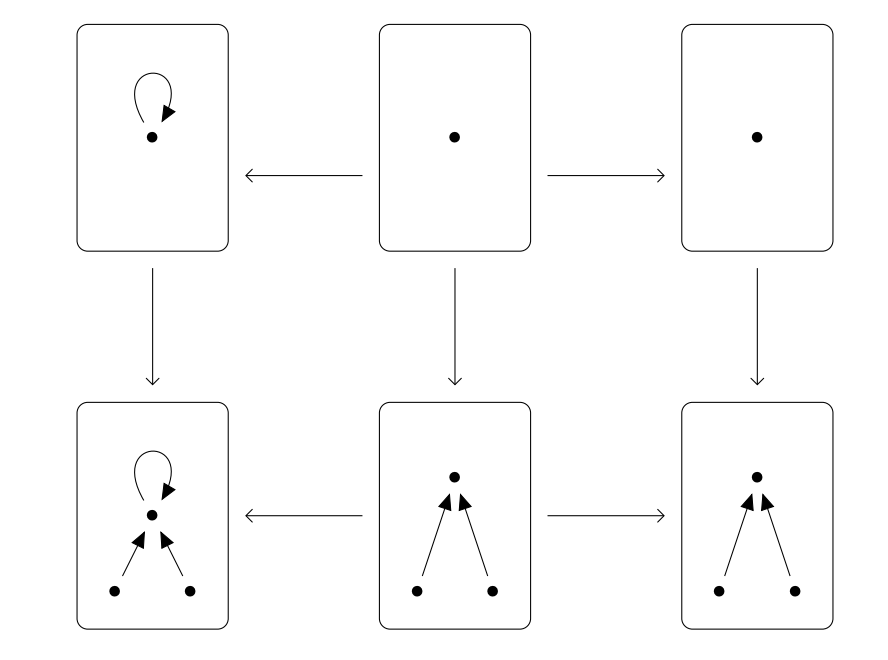
Structural Model Changes¶
Modifying models using a Grammar of rewrite rules.
Double Push Outs over structured cospans (Cicala Thesis, 2019)
Petrinet Model¶
using Petri
function main()
@variables S, I, R
N = +(S,I,R)
Δ = [(S+I, 2I),
(I, R),]
m = Petri.Model(Δ)
p = Petri.Problem(m, SIRState(100, 1, 0), 50)
soln = Petri.solve(p)
(p, soln)
end
p, soln = main()
SIR -> SIRS¶
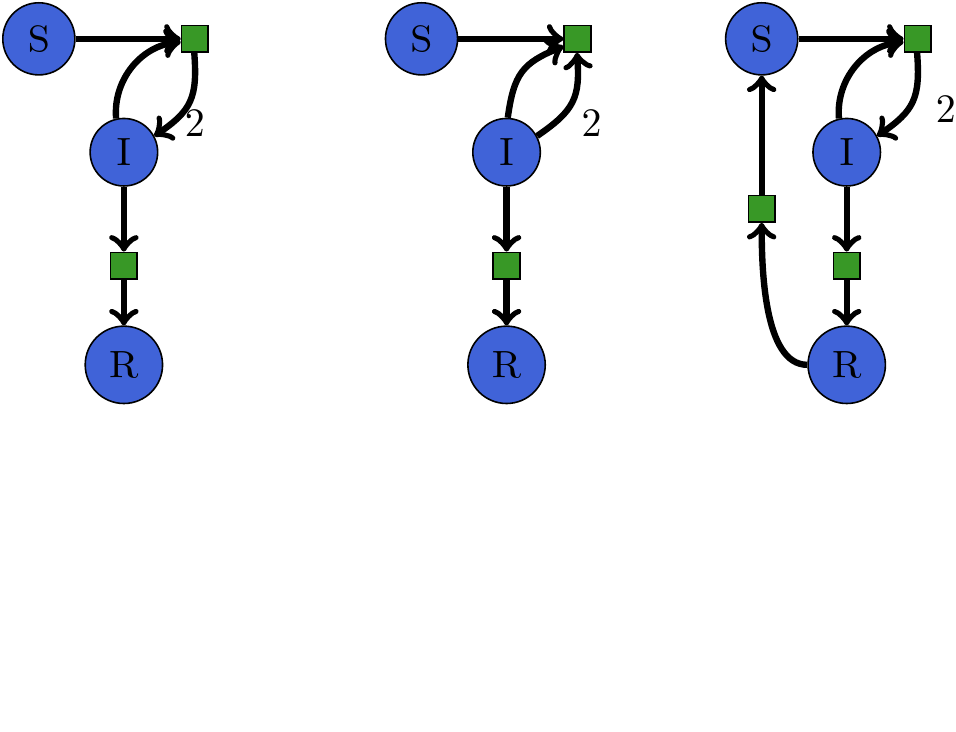
SIRS model as code¶
using Petri
function main()
@variables S, I, R
N = +(S,I,R)
Δ = [(S+I, 2I),
(I, R),
(R, S)]
m = Petri.Model(Δ)
p = Petri.Problem(m, SIRState(100, 1, 0), 50)
soln = Petri.solve(p)
(p, soln)
end
p, soln = main()
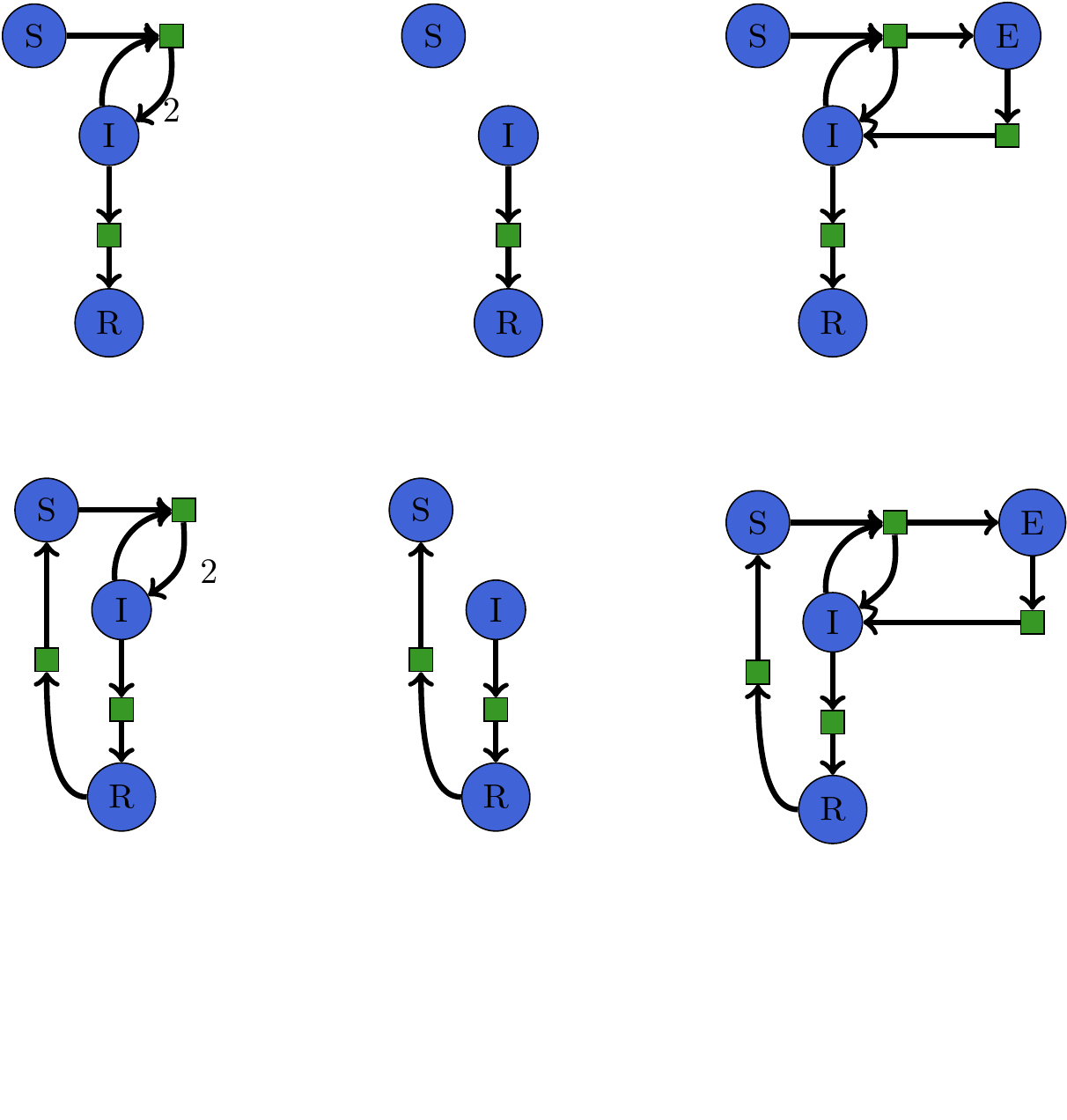
Software Interface for Rewriting Models¶
states = [S, I, R]
sir = Petri.Model(states,[(I, R), (S+I, 2I)])
ir = Petri.Model(states, [(I, R)])
seir = Petri.Model(states, [(I, R), (S+I, I+E), (E, I)])
rule = Span(sir, ir, seir)
# the root of the bottom of DPO
irs = Petri.Model(states, [(I, R), (R, S)])
sirs, seirs = solve(DPOProblem(rule, irs))
SEIRS Model as Declarative Code¶
using Petri
function SEIRSmain()
@variables S, E, I, R
N = +(S,E,I,R)
Δ = [(S+I, I+E),
(E, I),
(I, R),
(R, S)
]
m = Petri.Model(Δ)
p = Petri.Problem(m, SEIRState(100, 0, 1, 0), 150)
soln = Petri.solve(p)
(p, soln)
end
p, soln = SEIRSmain()
SEIRS Model as Imperative Code¶
:(##δ#754(state) = begin
begin
begin
state.I > 0 || return nothing
state.I -= 1
end
state.R += 1
end
end)
:(##δ#755(state) = begin
begin
begin
state.S > 0 || return nothing
state.I > 0 || return nothing
state.S -= 1
state.I -= 1
end
begin
state.I += 1
state.E += 1
end
end
end)
:(##δ#756(state) = begin
begin
begin
state.E > 0 || return nothing
state.E -= 1
end
state.I += 1
end
end)
:(##δ#757(state) = begin
begin
begin
state.R > 0 || return nothing
state.R -= 1
end
state.S += 1
end
end)
Compiler / Disassembler¶
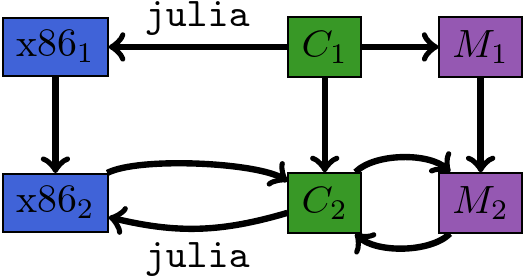 Module Augmentation as a Lens
Module Augmentation as a Lens
SEIRS Model as x86 Assembly¶
A tiny portion of the model!
.section __TEXT,__text,regular,pure_instructions
; Function ##δ#788 {
; Location: rewrite.jl:127
; Function getproperty; {
; Location: rewrite.jl:148
decl %eax
movl 8(%esi), %eax
;}
; Function >; {
; Location: operators.jl:286
; Function <; {
; Location: int.jl:49
decl %eax
testl %eax, %eax
;}}
jle L37
; Function -; {
; Location: int.jl:52
decl %eax
addl $-1, %eax
;}
; Function setproperty!; {
; Location: sysimg.jl:19
decl %eax
movl %eax, 8(%esi)
;}
; Function getproperty; {
; Location: sysimg.jl:18
decl %eax
movl 16(%esi), %eax
;}
; Function +; {
; Location: int.jl:53
decl %eax
addl $1, %eax
;}
; Function setproperty!; {
; Location: sysimg.jl:19
decl %eax
movl %eax, 16(%esi)
;}
decl %eax
movl %eax, (%edi)
movb $2, %dl
xorl %eax, %eax
retl
L37:
movb $1, %dl
xorl %eax, %eax
; Location: rewrite.jl:127
retl
nopw (%eax,%eax)
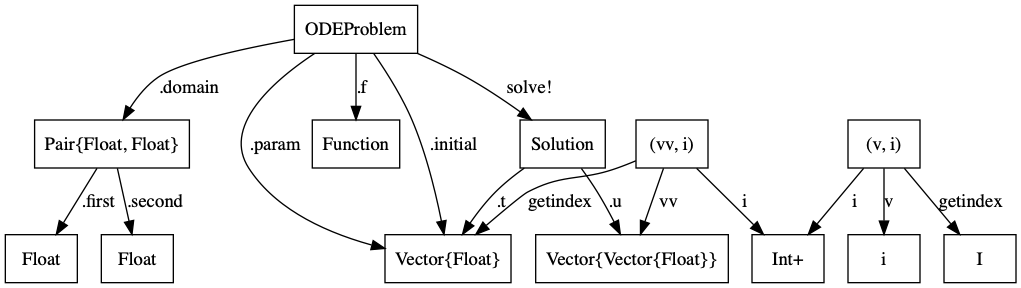
;}Compiling Petri.Model to ODEProblem¶
f(du, state, p, t) = begin
du.S = (-p[1] * (((state.β * state.S) * state.I)
/ ((state.S + state.I) + state.R)))
+ p[3] * (state.μ * state.R)
du.I = (p[1] * (((state.β * state.S) * state.I)
/ ((state.S + state.I) + state.R)))
+ -p[2] * (state.γ * state.I)
du.R = ((p[2] * (state.γ * state.I))
+ -p[3] * (state.μ * state.R))
end
function main()
param = [0.1,0.05]
init = [0.99,0.01,0.0]
tspan = (0.0,200.0)
prob = ODEProblem(f, init, tspan, param)
sol = solve(prob);
end
Functorial Semantics?¶
Can we make this rigorous?

Conclusion¶
SemanticModels.jl github.com/jpfairbanks/SemanticModels.jl is a foundational technology for teaching machines to reason about scientific models
SemanticModels.jl combines DPO rewriting with Lenses for model augmentation for science!
$SemanticModels = Codification \circ Categorification \circ Science $
Open Questions¶
- Which scientific modeling frameworks can be categorified?
- How can we compute DPO rewriting for general categories?
- What other modeling activities have CT formalizations?
Acknowledgements¶

