SemanticModels.jl: Not Just Another Modeling Framework¶
James Fairbanks & Christine Herlihy
JuliaCon2019

- Teaching computers to do science
- Project Repo github.com/jpfairbanks/SemanticModels.jl
Scientific Modeling¶
- Scientists make models out of math
- Models need to be implemented as code
- When you change the math, you need to change the code!
Modeling Frameworks¶
Most frameworks are designed before the models are written
| Framework | Math | Input Specification | Description |
|---|---|---|---|
 Matlab/Scipy Matlab/Scipy |
x = A\b | BLAS + scripting | Sci/Eng math is all BLAS |
 Mathematica Mathematica |
$p(x)=0$ | Symbolic Math Expressions | Computer Algebra Systems |
 Stan Stan |
$ y \sim \mathcal{N}(x \beta + \alpha, \sigma)$ | StanML | Bayesian Inference |
| $\min_{x\perp C(x)} f(x)$ | AMPL based DSL | Optimization Problems | |
 |
$y\approx f(x)$ | TF.Graph | Deep Learning |
 SemanticModels.jl SemanticModels.jl |
All Computable Domains | Julia Programs | $Models \subset Code$ |
SemanticModels is a post hoc modeling framework
What is a Modeling Framework?¶
- Objects: $X,Y,Z$
- Models: $f:X\rightarrow Y$, $g: Y\rightarrow Z$
- Composition: $g\circ f: X\rightarrow Z$
- Combination: $f\otimes g: X\otimes Y \rightarrow Y\otimes Z$
- Executability: $\texttt{foo} = eval(f) \implies \texttt{foo(x::X)::Y}$ runs the model
Mathematical Diagrams are pervasive¶
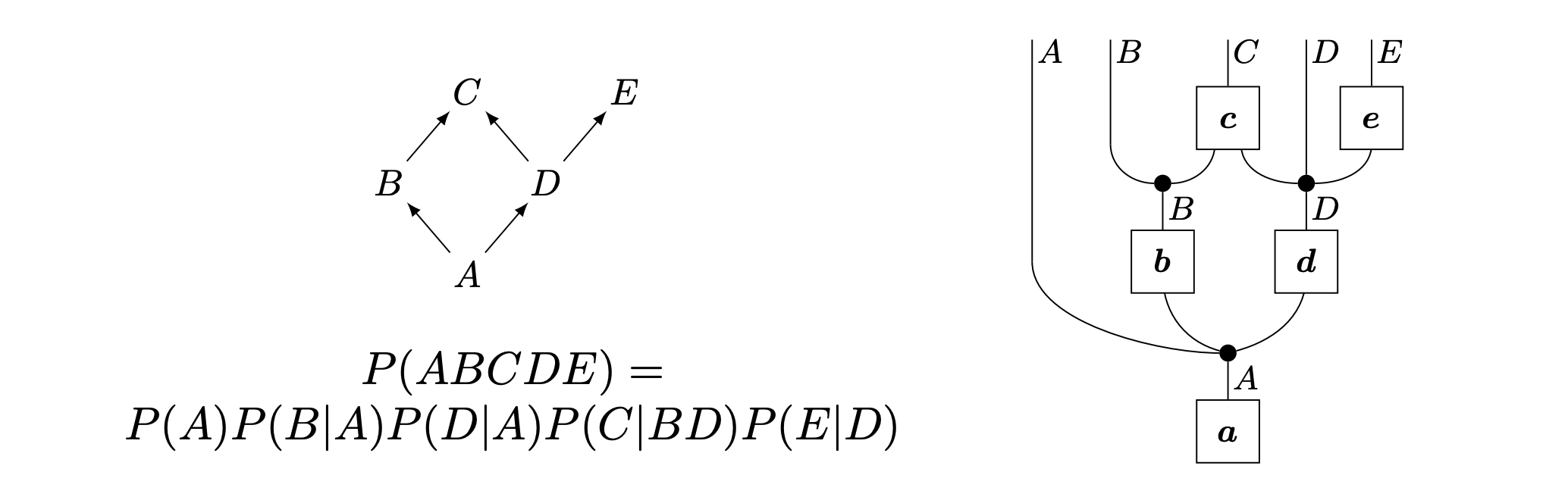 Two perspectives on Bayesian Networks (Jacobs, Kissinger, and Zanasi, 2019)
Two perspectives on Bayesian Networks (Jacobs, Kissinger, and Zanasi, 2019)Scientists love diagrams¶
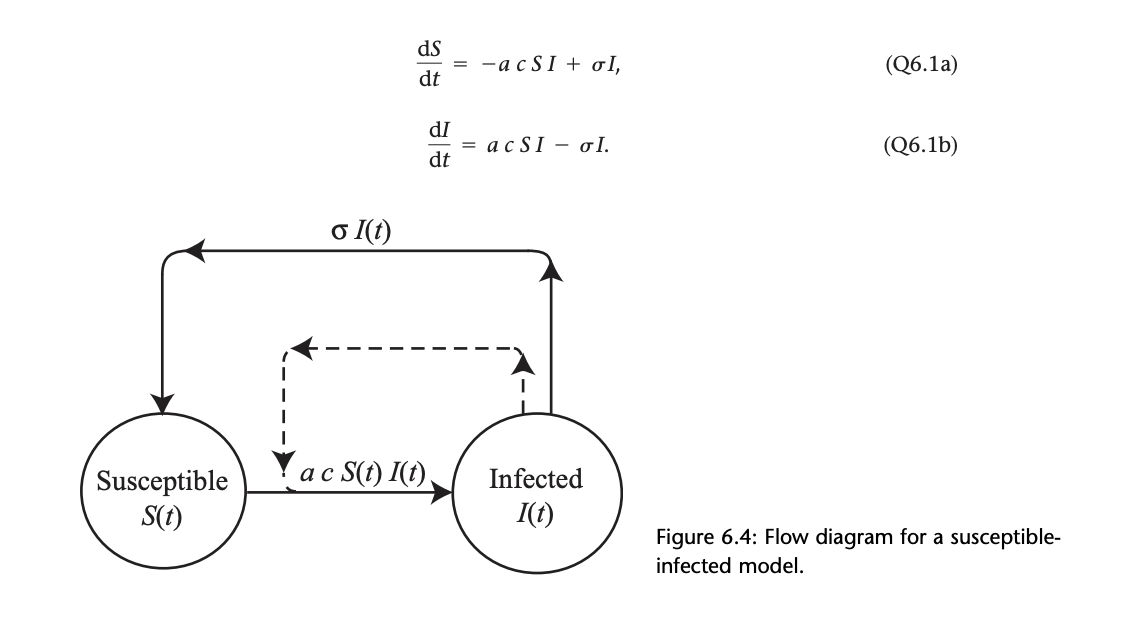 The SIS Model (figure from A Biologist's guide to Mathematical Modeling in Ecology and Evolution By Sarah Otto and Troy Day 2007)
The SIS Model (figure from A Biologist's guide to Mathematical Modeling in Ecology and Evolution By Sarah Otto and Troy Day 2007)
SIR model of disease¶
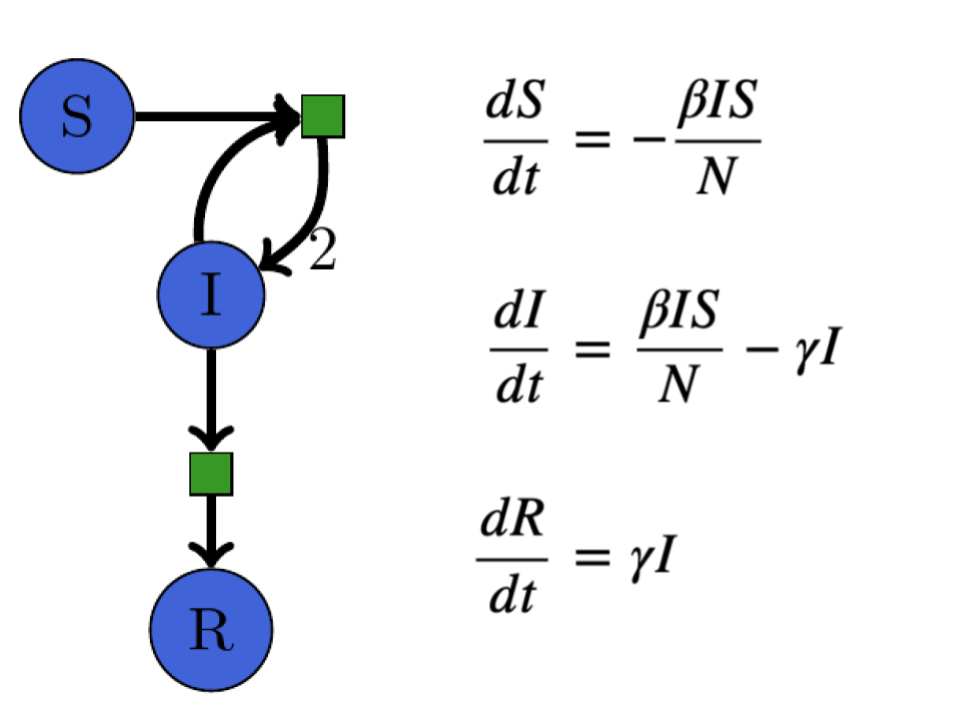 The SIR model shown with equivalent Petri net and system of ODEs
The SIR model shown with equivalent Petri net and system of ODEs
SIR predicts real diseases¶
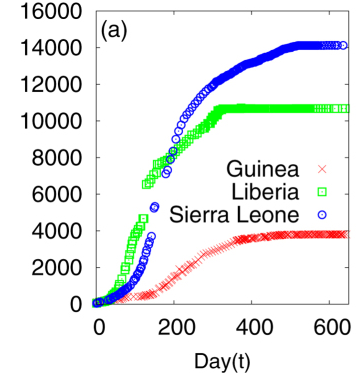 Ebola Outbreak Data
Ebola Outbreak Data
(a) Cumulative number of infected individuals as a function of time (day) for the three countries Guinea, Liberia and Sierra Leone.
A Khalequea, and P Senb, "An empirical analysis of the Ebola outbreak in West Africa" 2017
ODE Based Implementation¶
This is a "real world" implementation of SIR modeling in Julia taken from Epirecipes Cookbook (Simon Frost)
module SIRModel
using DifferentialEquations
function sir_ode(du, u, p, t)
#Infected per-Capita Rate
β = p[1]
#Recover per-capita rate
γ = p[2]
#Susceptible Individuals
S = u[1]
#Infected Individuals
I = u[2]
du[1] = -β * S * I
du[2] = β * S * I - γ * I
du[3] = γ * I
end
#Param = (Infected Per Capita Rate, Recover Per Capita Rate)
param = [0.1,0.05]
#Initial Params = (Susceptible Individuals, Infected by Infected Individuals)
init = [0.99,0.01,0.0]
tspan = (0.0,200.0)
sir_prob = ODEProblem(sir_ode, init, tspan, param)
sir_sol = solve(sir_prob, saveat = 0.1);
Agent based simulation¶
""" Agent Models is a hypothetical ABM framework"""
module AgentModels
abstract type AgentModel end
mutable struct StateModel{T} <: AgentModel
states::Vector{Symbol}
data::T
events::Vector{Function}
rates::Vector{Number}
end
solve(m::StateModel) = return thesolution(m)
end
using AgentModels #hypothetical ABM framework
function main(nsteps)
function infection(s)
if s.S > 0 && s.I > 0
s.S -= 1
s.I -= 1
s.I += 2
end
end
function recovery(s)
if s.I > 0
s.I -= 1
s.R += 1
end
end
states = [:S, :I, :R]
a = zeros(Int, states)
ρ = 0.5 + randn(Float64)/4 # chance of recovery
μ = 0.5 # chance of immunity
T = [infection, recovery]
prob = StateModel(states, a, T, [ρ, μ])
soln = solve!(sam, nsteps)
return soln
end
Model Augmentation as a Lens¶
We want scientists to program using lenses
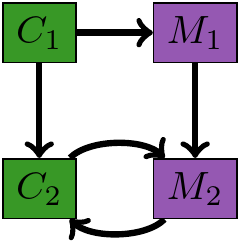 Module Augmentation as a Lens
Module Augmentation as a Lens
What should the $M_1, M_2$ be?
A Story of an Infectious Disease¶

A Story of an Infectious Disease¶

A Story of an Infectious Disease¶

Wiring Diagrams are a universal syntax¶
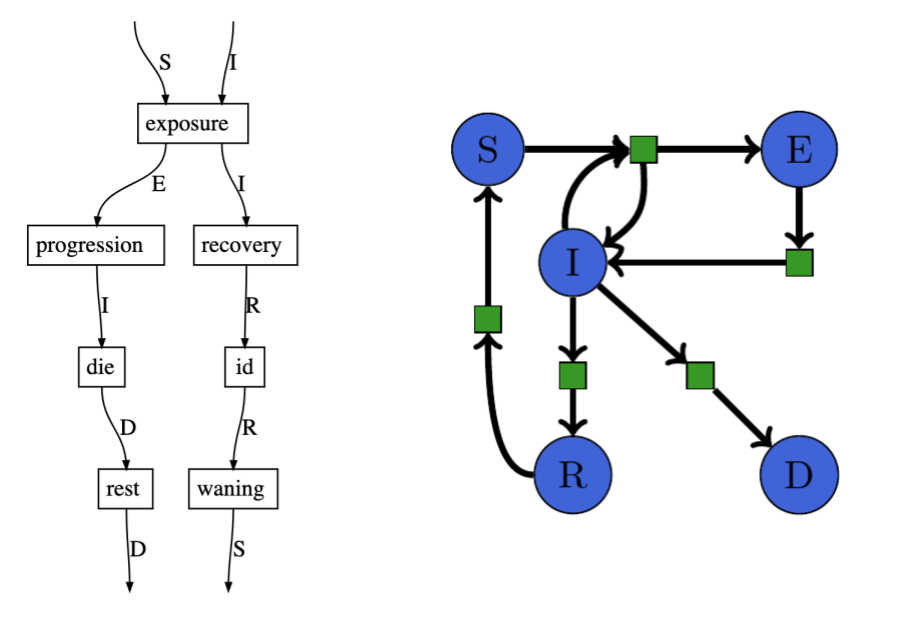 Associate all wires with the same label to get a petri net
Associate all wires with the same label to get a petri net
Petrinet SIR Model¶
using Petri
function main()
@variables S, I, R
N = +(S,I,R)
Δ = [(S+I, 2I),
(I, R)]
m = Petri.Model(Δ)
p = Petri.Problem(m, SIRState(100, 1, 0), 50)
soln = Petri.solve(p)
(p, soln)
end
p, soln = main()
Type Graphs¶
- The TypeGraph of a Julia Program tells you a lot about it
- Computers are good at type checking
- Can we embed our modeling semantics into the type system?
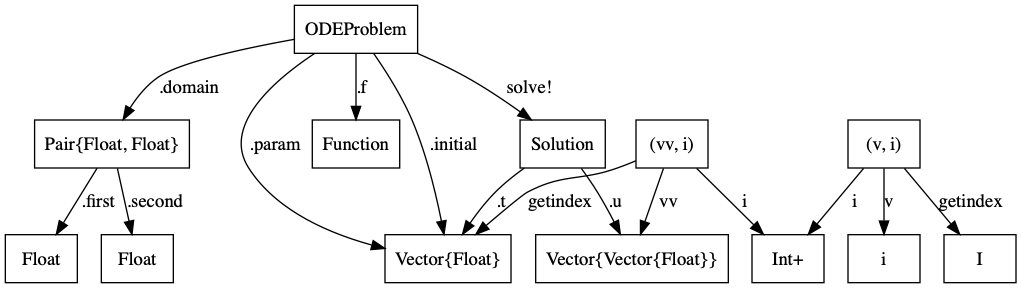
Structural Model Changes¶
Modifying models using a Grammar of rewrite rules.
Reasoning by analogy
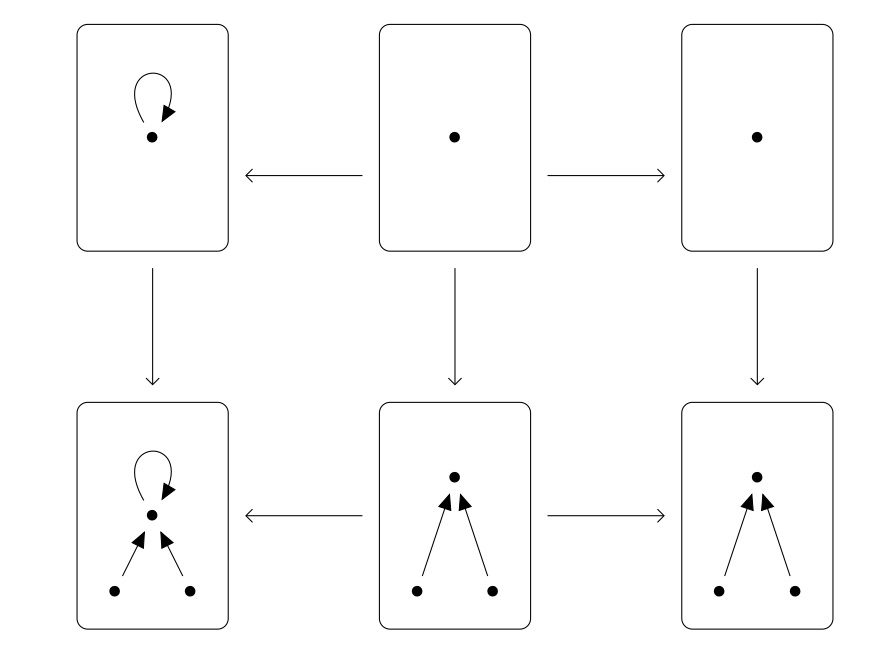 Double Push Outs over structured cospans (figure from Cicala, 2019)
Double Push Outs over structured cospans (figure from Cicala, 2019)
Petrinet Model¶
using Petri
function main()
@variables S, I, R
N = +(S,I,R)
Δ = [(S+I, 2I),
(I, R),]
m = Petri.Model(Δ)
p = Petri.Problem(m, SIRState(100, 1, 0), 50)
soln = Petri.solve(p)
(p, soln)
end
p, soln = main()
SIR -> SIRS¶
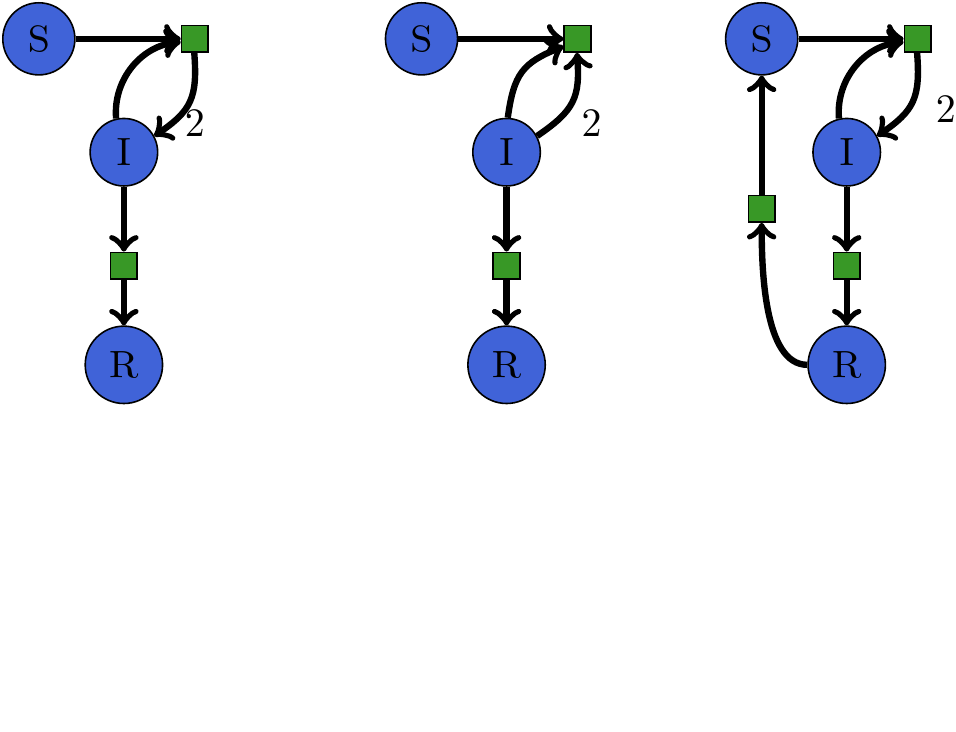
SIRS model as code¶
using Petri
function main()
@variables S, I, R
N = +(S,I,R)
Δ = [(S+I, 2I),
(I, R),
(R, S)]
m = Petri.Model(Δ)
p = Petri.Problem(m, SIRState(100, 1, 0), 50)
soln = Petri.solve(p)
(p, soln)
end
p, soln = main()
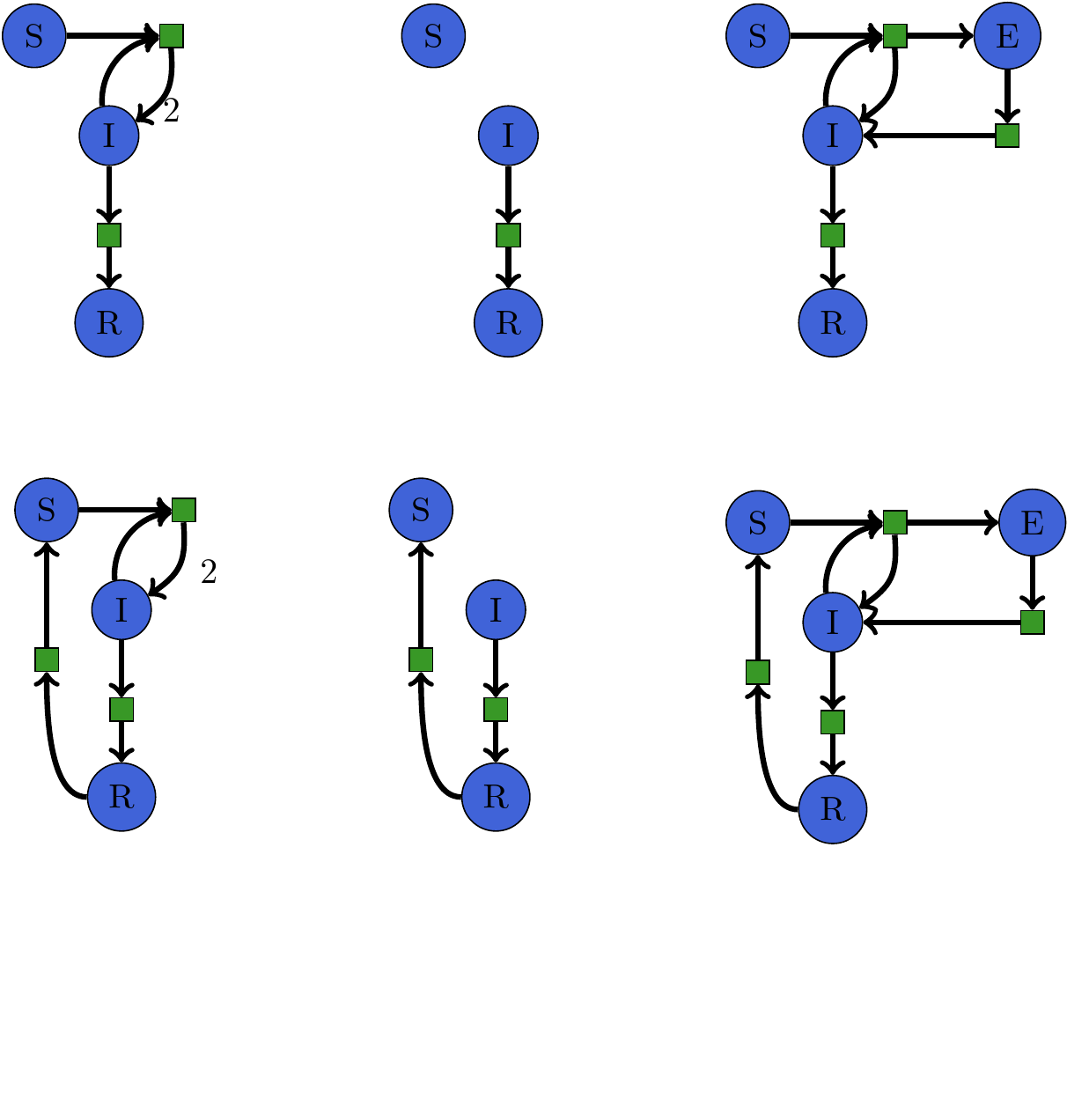
Software Interface for Rewriting Models¶
states = [S, I, R]
sir = Petri.Model(states,[(I, R), (S+I, 2I)])
ir = Petri.Model(states, [(I, R)])
seir = Petri.Model(states, [(I, R), (S+I, I+E), (E, I)])
rule = Span(sir, ir, seir)
# the root of the bottom of DPO
irs = Petri.Model(states, [(I, R), (R, S)])
sirs, seirs = solve(DPOProblem(rule, irs))
Rewriting Models is a modeling framework¶
 We can recursively define a modeling framework for modeling frameworks!
We can recursively define a modeling framework for modeling frameworks!
SEIRS Model as Declarative Code¶
using Petri
function SEIRSmain()
@variables S, E, I, R
N = +(S,E,I,R)
Δ = [(S+I, I+E),
(E, I),
(I, R),
(R, S)
]
m = Petri.Model(Δ)
p = Petri.Problem(m, SEIRState(100, 0, 1, 0), 150)
soln = Petri.solve(p)
(p, soln)
end
p, soln = SEIRSmain()
SEIRS Model as Imperative Code¶
:(##δ#754(state) = begin
begin
begin
state.I > 0 || return nothing
state.I -= 1
end
state.R += 1
end
end)
:(##δ#755(state) = begin
begin
begin
state.S > 0 || return nothing
state.I > 0 || return nothing
state.S -= 1
state.I -= 1
end
begin
state.I += 1
state.E += 1
end
end
end)
:(##δ#756(state) = begin
begin
begin
state.E > 0 || return nothing
state.E -= 1
end
state.I += 1
end
end)
:(##δ#757(state) = begin
begin
begin
state.R > 0 || return nothing
state.R -= 1
end
state.S += 1
end
end)
Modeling Frameworks¶
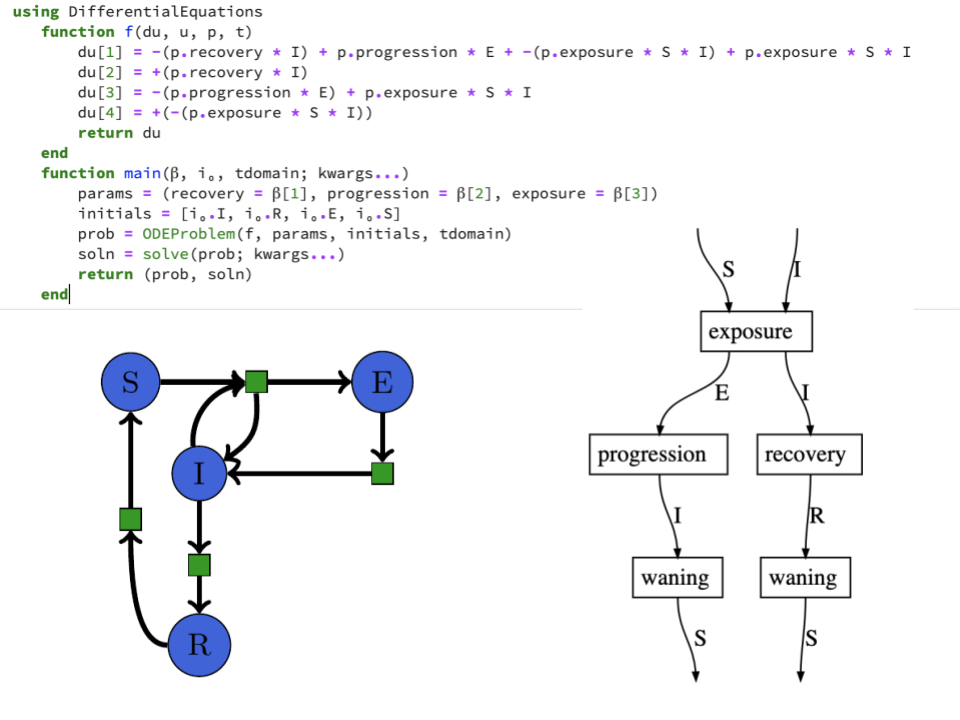
Lenses + Rewriting¶
Conclusion¶
SemanticModels.jl github.com/jpfairbanks/SemanticModels.jl is a foundational technology for teaching machines to reason about scientific models
SemanticModels.jl combines DPO rewriting with Lenses for model augmentation for science!
$SemanticModels = Codification \circ Categorification \circ Science $
Open Questions¶
- Which scientific modeling frameworks can we represent?
- How can we compute rewriting for general frameworks?
- What other modeling activities can we formalize?
Acknowledgements¶
