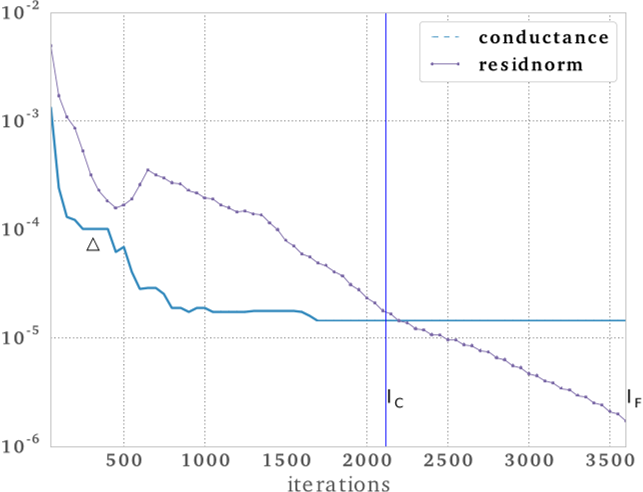

Spectral partitioning (clustering) algorithms use eigenvectors to solve network analysis problems. The relationship between numerical accuracy and network mining quality is insufficiently understood. We show that analyzing numerical accuracy and network mining quality together leads to an algorithmic improvement. Specifically, we study spectral partitioning using sweep cuts of approximate eigenvectors of the normalized graph Laplacian. We introduce a novel, theoretically sound, parameter free stopping criterion for iterative eigensolvers designed for graph partitioning. On a corpus of social networks, we validate this stopping criterion by showing the number of iterations is reduced by a factor of 4.15 on average, and the conductance is increased by only a factor of 1.24 on average. Regression analysis of these results shows that the decrease in the number of iterations needed is greater for problems with a small spectral gap, thus our stopping criterion helps more on harder problems. Experiments show that alternative stopping criteria are insufficient to ensure low conductance partitioning on real world networks. While our method guarantees partitions that satisfy the Cheeger Inequality, we find that it typically beats this guarantee on real world graphs.