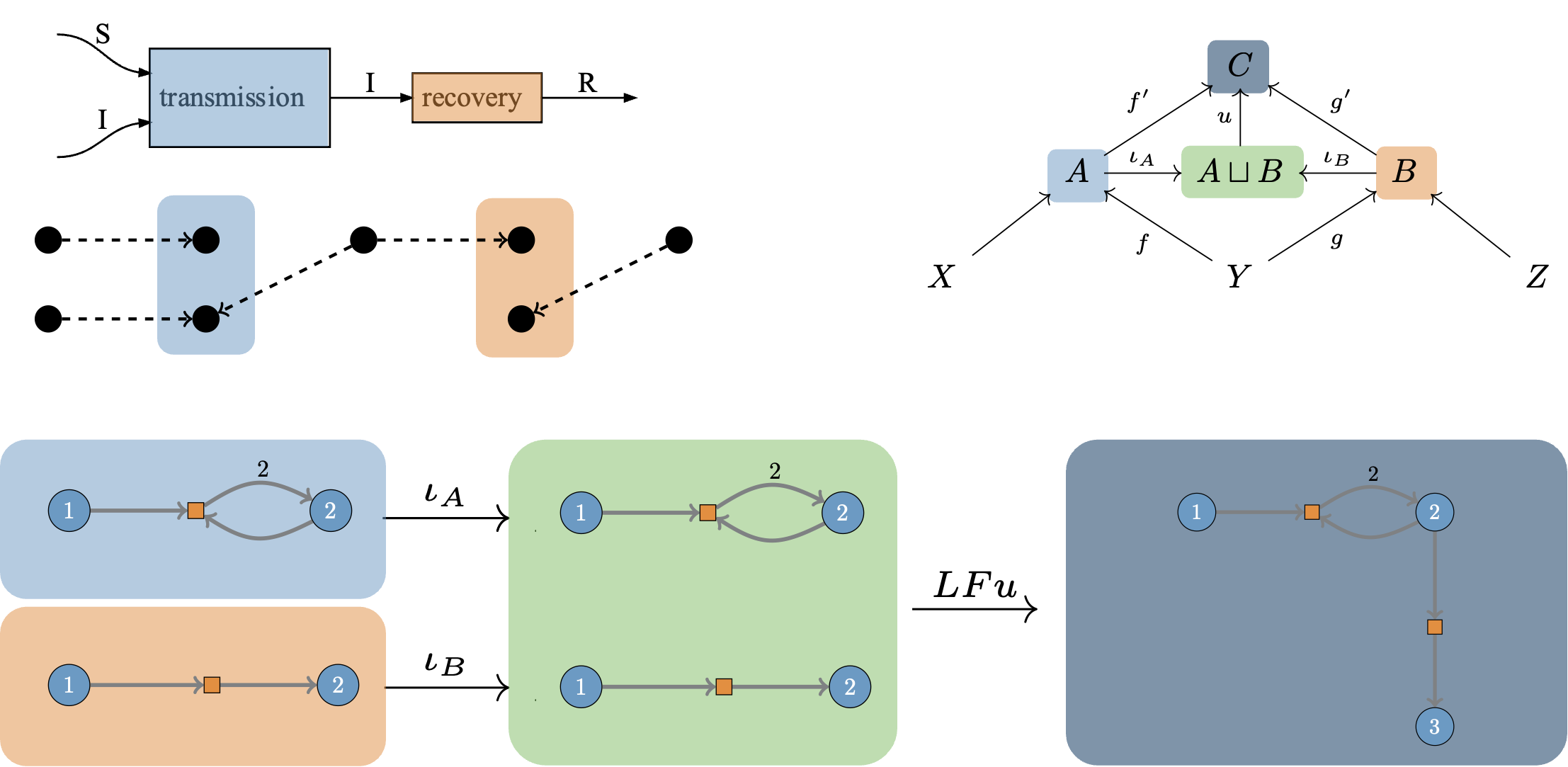
I’ve started the AlgebraicJulia blog with Evan Patterson and the rest of the AlgebraicJulia team, so you can find my recent essays there. A particularly interesting piece is some work with Sophie Libkind on compositional dynamical systems.
Research
Software and Data

AlgebraicJulia
AlgebraicJulia is an ecosystem of software tools written in Julia to explore and promote the application of algebraic methods in computer science and scientific computing.
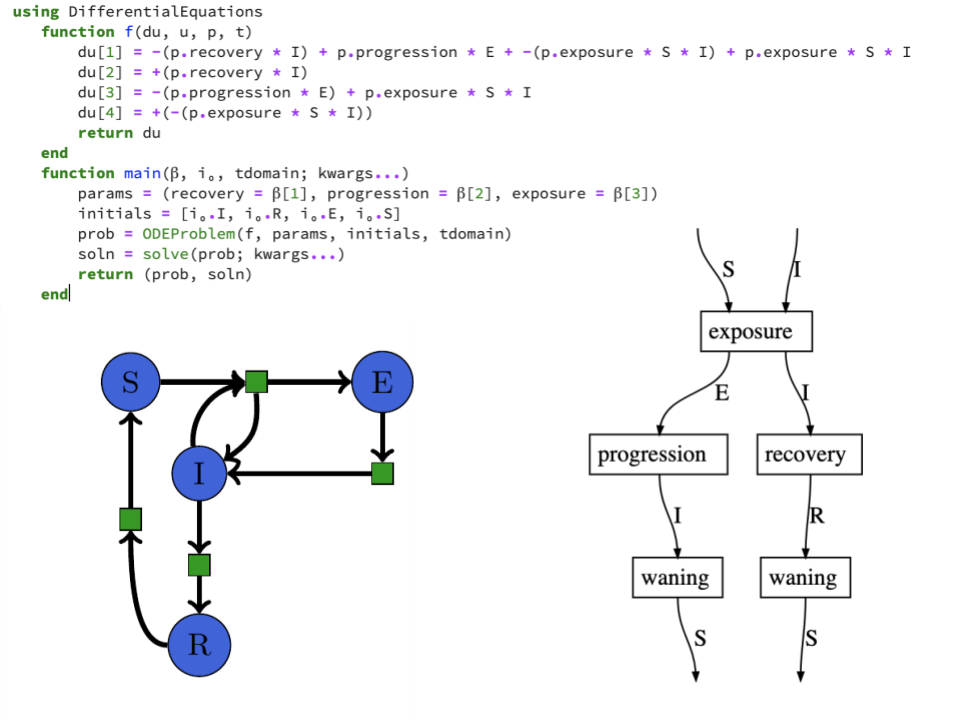
SemanticModels.jl
SemanticModels.jl is a package for representing scientific models at the semantic level to enable augmented scientific reasoning. It applies techniques from applied category theory to build mathematical models of scientific modeling practices.
Julia Graphs
JuliaGraphs is the primary organization dedicated to the advancement of graph theory and algorithms in the Julia Programming language. The flagship project is LightGraphs.jl the premier graph library in the Julia Ecosystem.
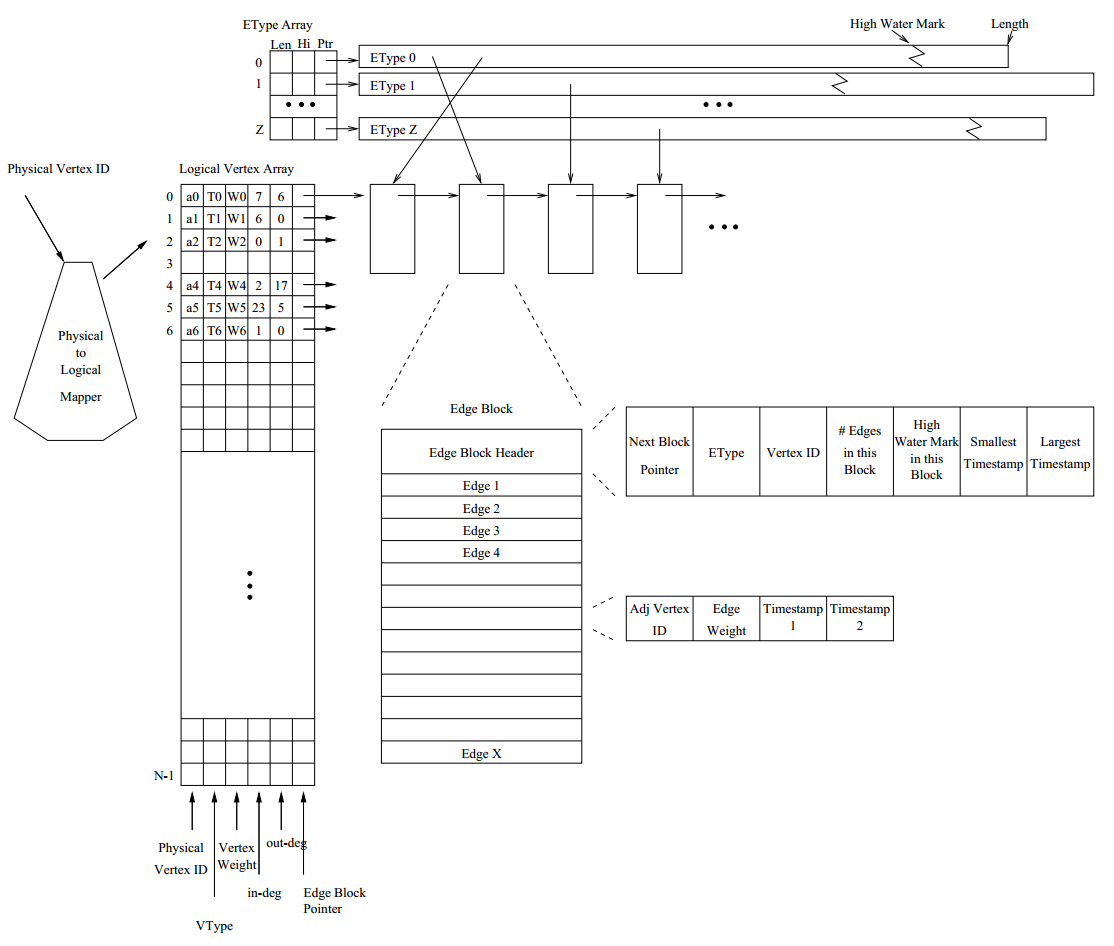
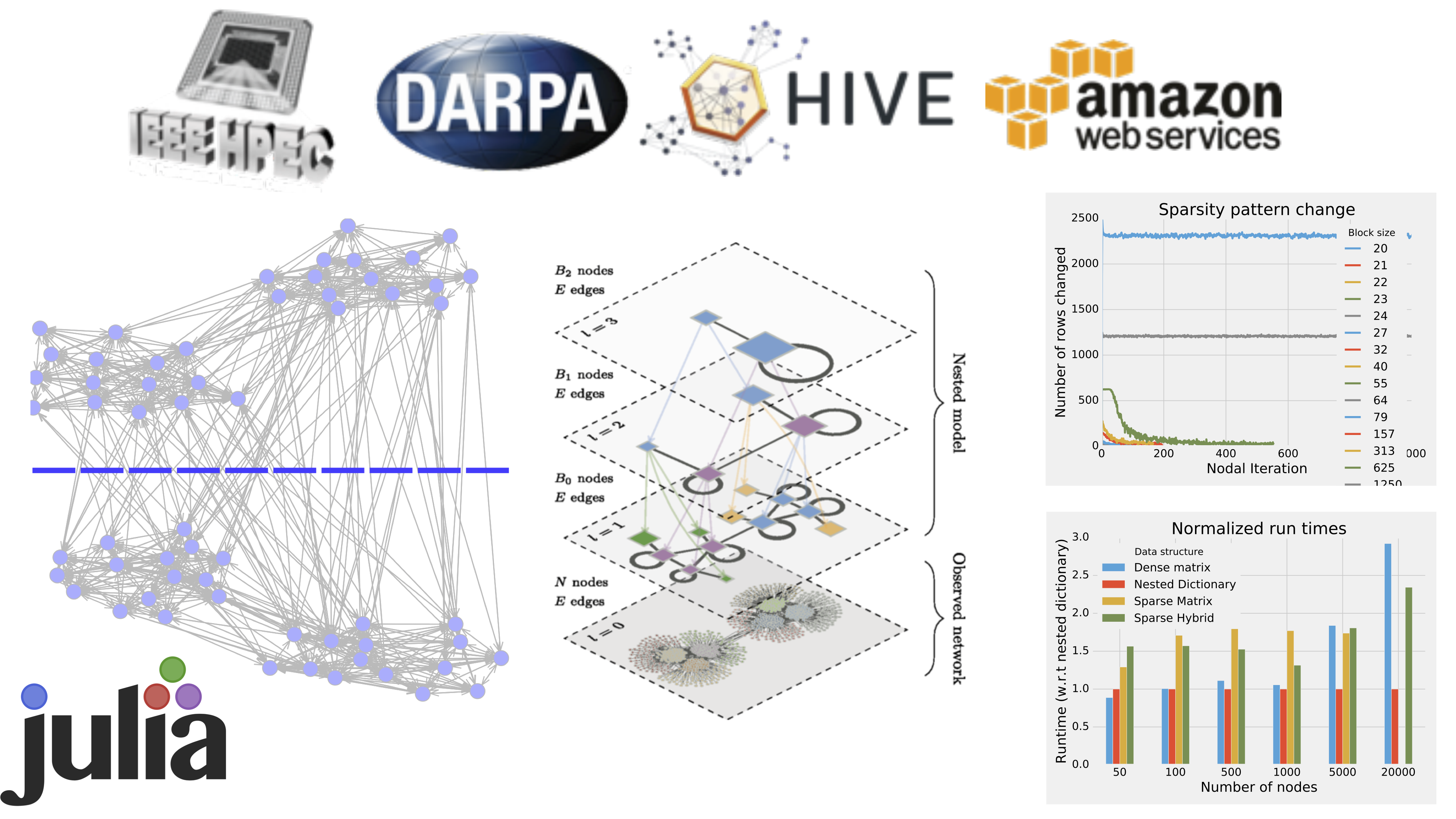
Stinger Graph Analysis
Dynamic graphs are all around us. Social networks containing interpersonal relationships and communication patterns. Information on the Internet, Wikipedia, and other datasources. Disease spread networks and bioinformatics problems. Business intelligence and consumer behavior. The right software can help to understand the structure and membership of these networks and many others as they change at speeds of thousands to millions of updates per second.